Ультразвуковая томография

Обратные задачи волновой томографии возникают в самых различных приложениях. К таким задачам относятся некоторые обратные задачи электромагнитного зондирования, сейсмики, инженерной сейсмики, гидролокации, диагностике промышленных изделий с помощью акустического излучения и т.п.

Одним из важнейших приложений волновой томографии является ультразвуковая томография в медицине. В первую очередь ультразвуковая томография призвана решать проблемы дифференциальной диагностики рака молочной железы – одной из самых актуальных проблем современной медицины. У более чем 40 % пациентов при первом обследовании молочной железы диагностируется рак поздней стадии.

В настоящее время в США, Германии, Японии и России интенсивно разрабатываются макеты ультразвуковых томографических установок [1, 2, 3], которые имеют целый ряд преимуществ в сравнении с магнитно-резонансной и рентгеновской томографиями. С математической точки зрения обратные задачи, возникающие в ультразвуковой томографии, являются намного более сложными по сравнению с обратными задачами рентгеновской томографии. В рентгеновской томографии хорошо работает модель геометрической оптики. Обратные задачи рентгеновской томографии являются линейными. Для их решения вполне достаточно обычного персонального компьютера.

В отличие от рентгеновской томографии, в ультразвуковой томографии используется как прошедшее, так и отраженное излучение, испущенное широкополосными источниками зондирующих импульсов. Источники и приемники располагаются со всех сторон от исследуемого объекта, регистрируемый сигнал записывается во времени, что дает возможность обрабатывать большой объем данных, позволяющий получать высокое разрешение.

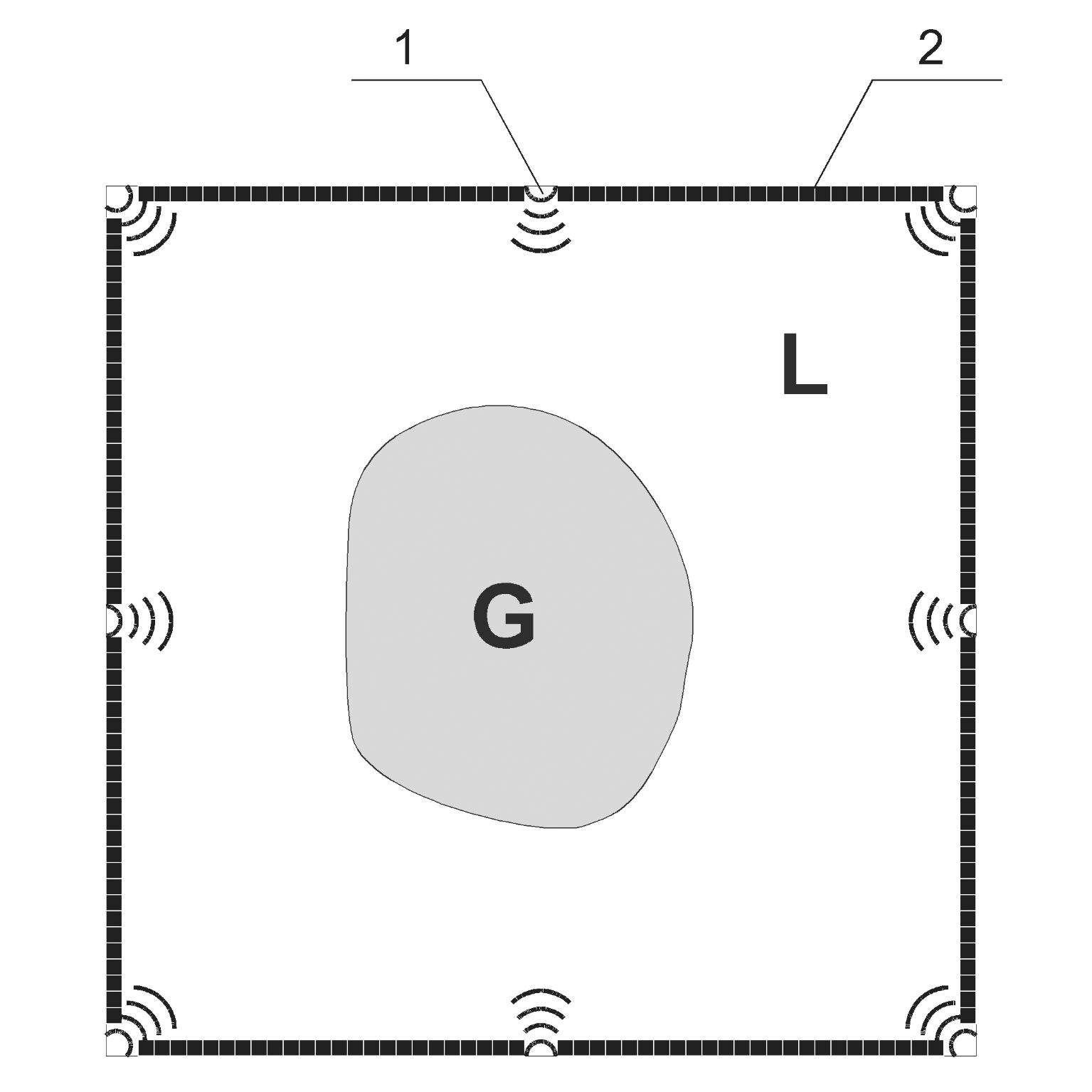
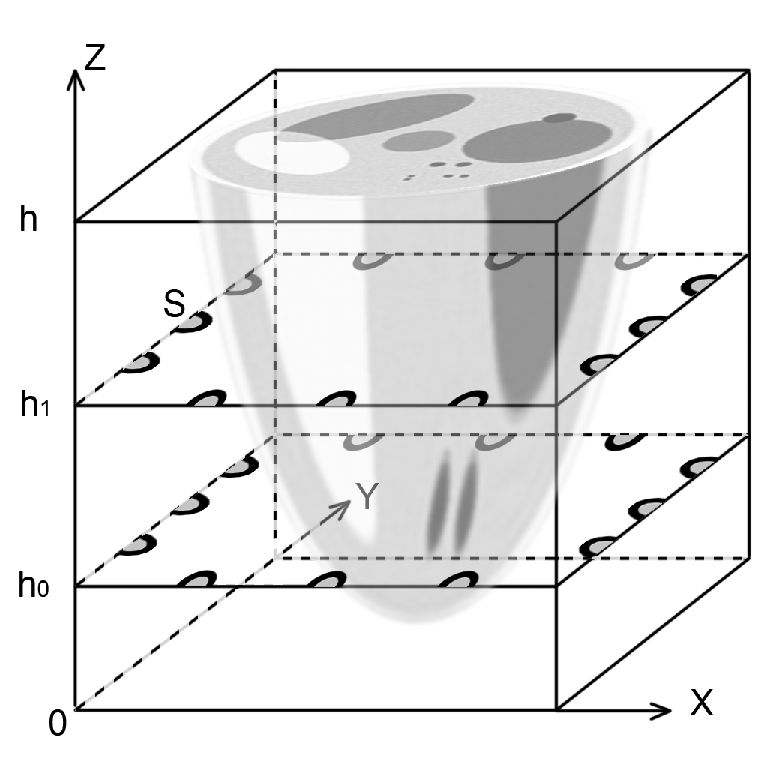
Обратные задачи ультразвуковой томографии можно рассматривать как коэффициентные обратные задачи. Приведем постановку обратной задачи. На Рис 1а приведена схемы томографических экспериментов при традиционной послойной 2.5D томографии, когда последовательно решаются двумерные задачи на слоях трехмерного объекта. На рис. 1б приведена схема 3D томографии, когда по собранным экспериментаьлным данным обратная задача решается сразу относительно трехмерной неизвестной функции c(r), r∊R³. На Рис.1а источники обозначены цифрой 1, a приемники, расположенные по периметру расчётной области – цифрой 2. На Рис.1б источники S и приемники ультразвуковых импульсов располагаются на гранях куба.

Рассмотрим волновое уравнение, которое описывает акустическое поле u(r,t) в области Ω⊂R^N, N=2,3, ограниченной поверхностью S в течение времени (0,T) с точечным источником, располагающимся в точке r₀ .

c(r)u_tt(r,t)-Δu(r,t)=δ(r-r₀)˙f(t)

u(r,t=0)=u_t(r,t=0)=0,   ∂_nu|_ST=p(r,t).

Здесь c^-0.5(r)=v(r) является неизвестной скоростью волны в диагностируемой области. Генерируемый источником импульс описывается заданной функцией f(t), ∂_nu|_ST - производная вдоль нормали к поверхности S в области S×(0,T), p(r,t) - некоторая известная функция. Будем предполагать, что неоднородность среды вызвана только изменениями скорости, а вне области неоднородности c(r)≡c₀=const, где c₀ - известна. Обратная задача состоит в нахождении функции c(r), описывающую неоднородность, по экспериментальным данным измерения акустического давления U(r,t) на границе S области Ω при различных положениях r₀ источника. Обратная задача является нелинейной. При решении обратной задачи ультразвуковой томографии на сетке 320х320х320 количество неизвестных превышает 10 миллионов.

Математически обратная задача ставится как задача минимизации функционала невязки Φ(u(c)) в норме пространства L₂ (S×(0,T)):

		T
Φ(u(c))=	1 2	∫	∫	(u(s,t)-U(s,t))2ds dt = ||u(s,t)-U(s,t)||2
		0	S

Прорывные результаты в области решения задач ультравзуковой томографии связаны с возможностью явно выписать выражение для градиента функционала невязки [4, 5, 6]. Предлагаемый в наших работах подход принципиально отличается от существующих разработок [1-3], в которых используются существенно более высокие частоты зондирования. Разработанные нами итерационные алгоритмы решения обратных задач ультразвуковой томографии и проведенные модельные исследования в широком диапазоне параметров позволяют в несколько раз снизить частоты зондирования. Этот момент является принципиальным поскольку поглощение в мягких тканях сильно зависит от частоты зондирования. Чем меньше частота, тем меньше поглощение, а следовательно и ошибка экспериментальных данных. Как показывают модельные эксперименты, при длине волны ультразвуковых волн порядка 5 мм можно достигать разрешение порядка 2-3 мм. В работе [7] предложены эффективные методы решения обратных задач УЗИ томографии в моделях, учитывающих поглощение в среде.

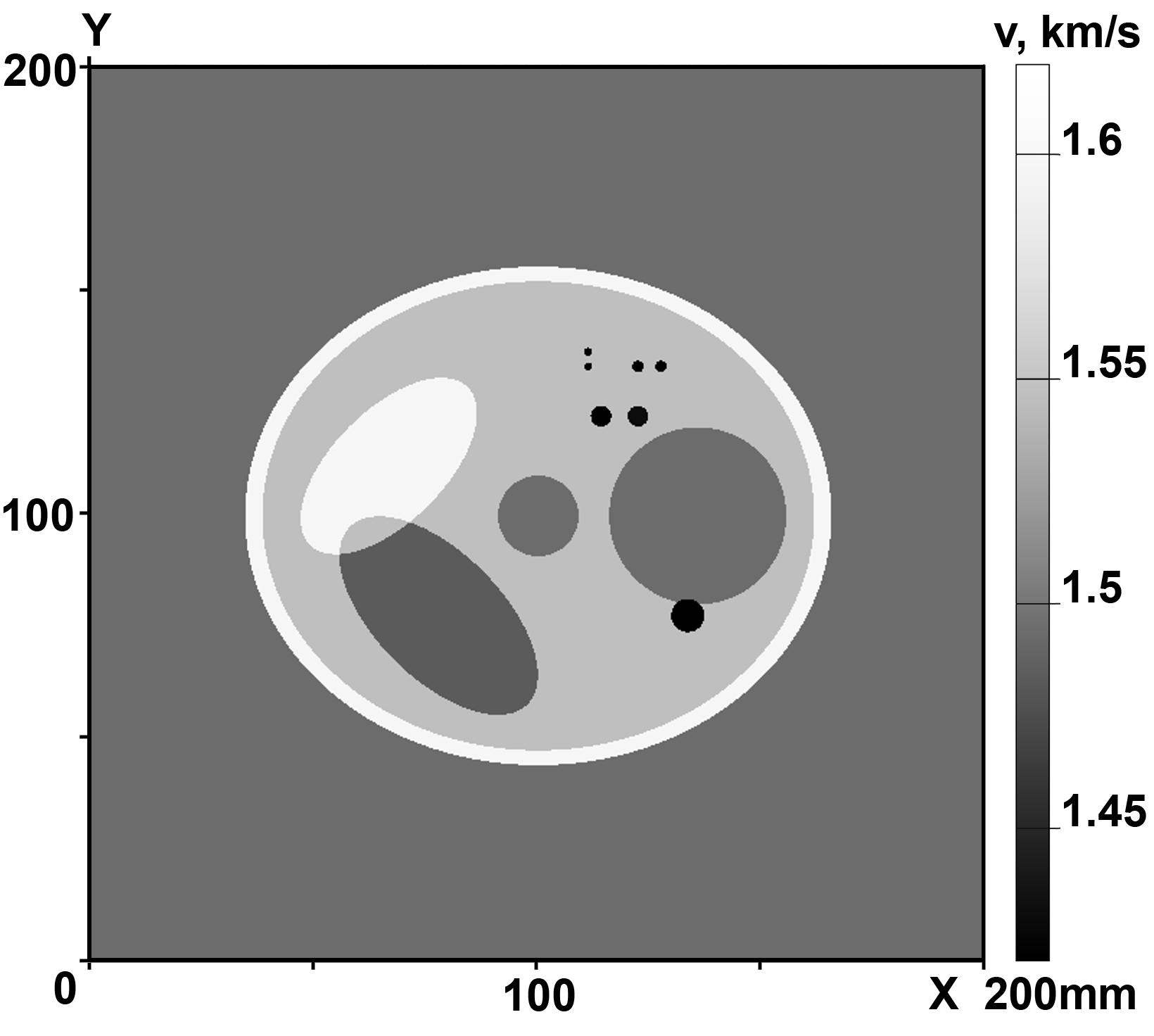
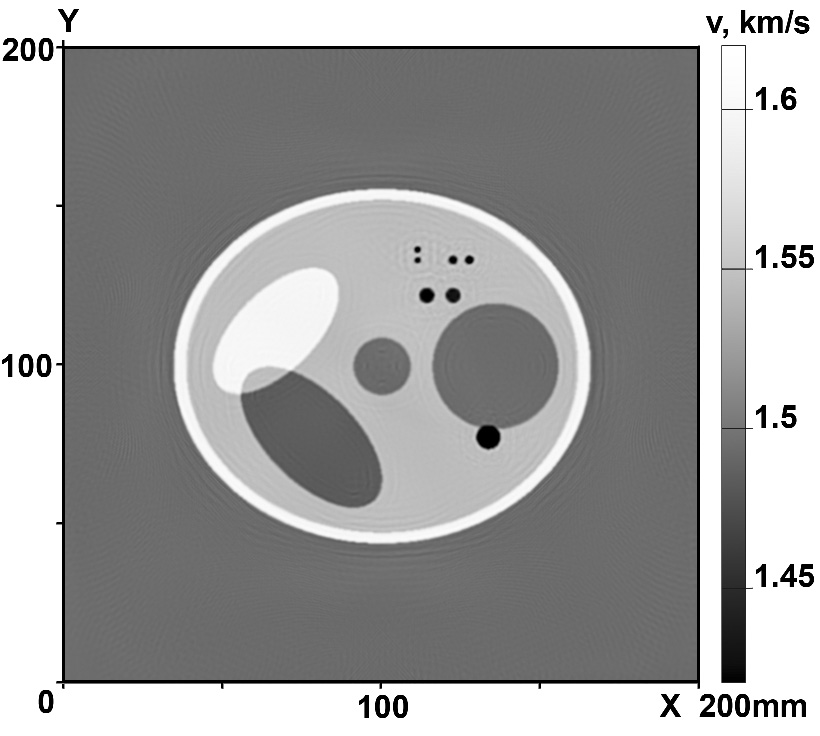
На рис.2 приведены результаты реконструкции для послойной 2.5D томографии. На рис.2а приведено изображение 2D фантома. На рис.2б приведены результаты реконструкции скорости звука без погрешности во входных данных. На рис.2в приведены результаты реконструкции при погрешности входных данных 1.5%. Модельные расчеты проводились для 8 источников. Расстояние между детекторами составляло 2.5 мм - половину длины волны. Размер области зондирования - 200×200 мм.

Минимальные размеры неоднородности на фантоме составляют порядка 2 мм. Из сопоставления исходного и восстановленных изображений видно, что полученная разрешающая способность не хуже 2-3 мм.

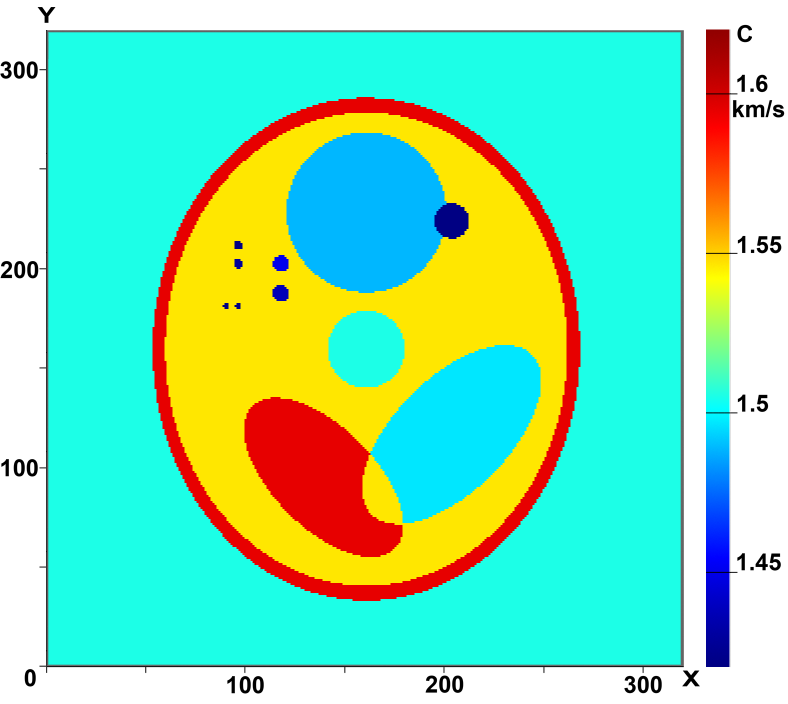
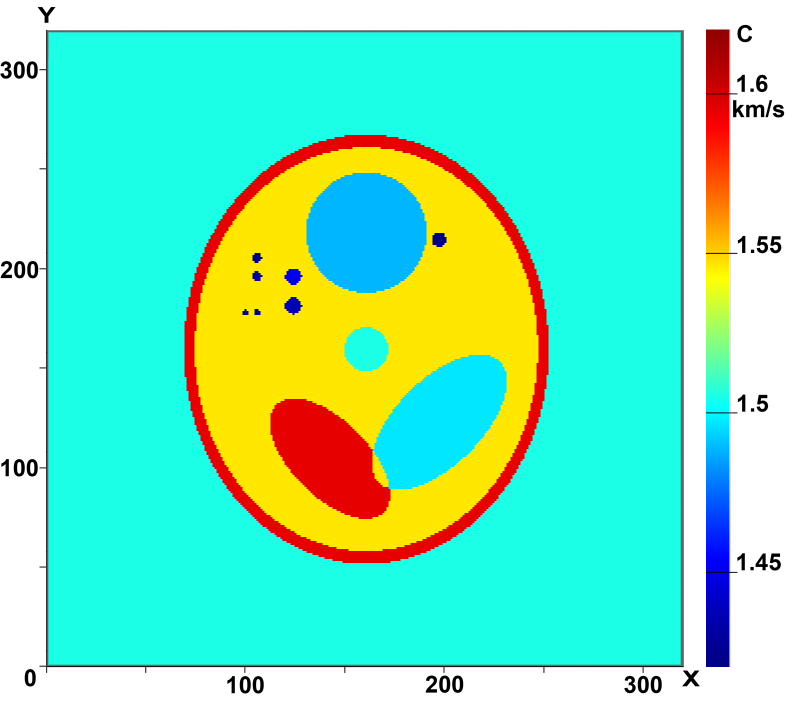
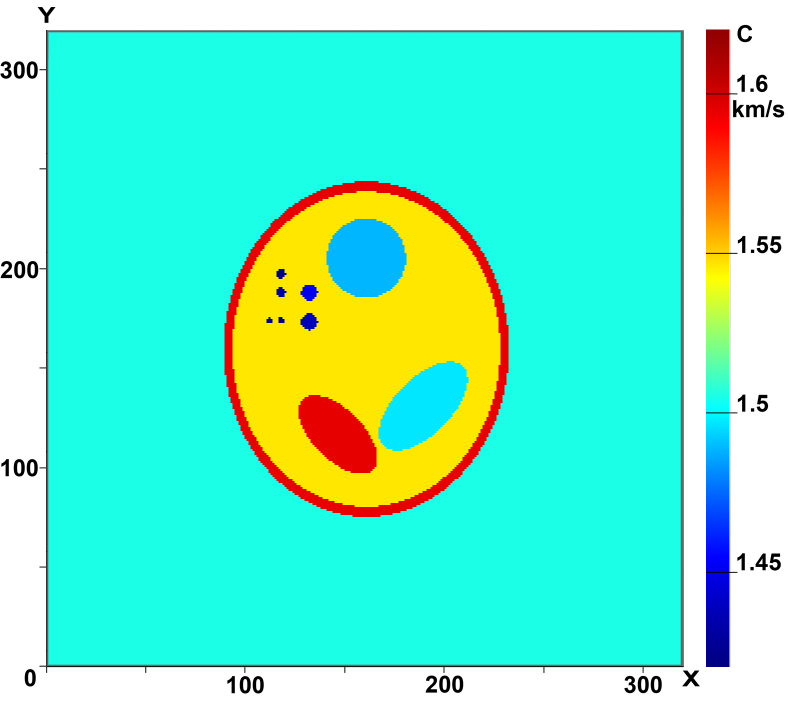
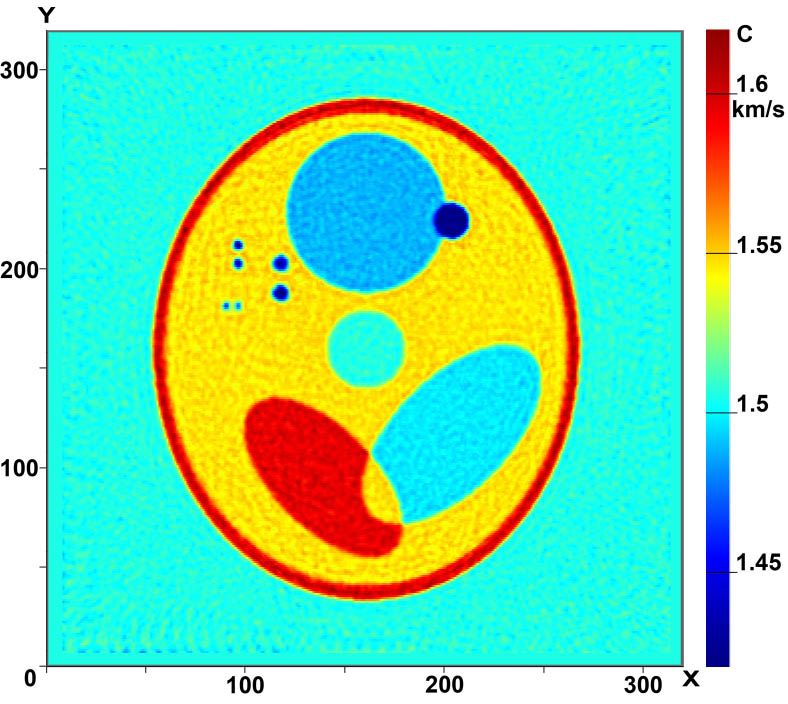
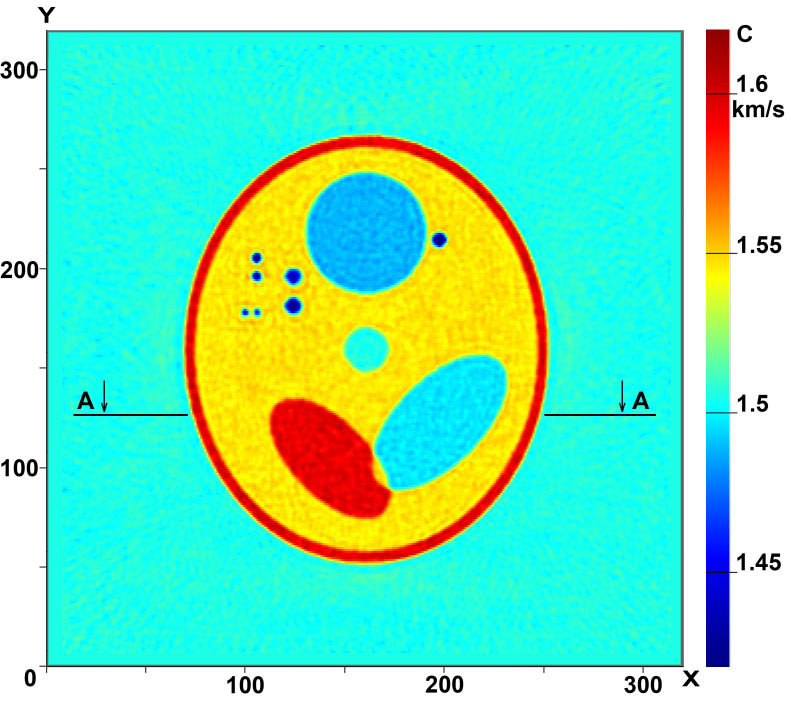
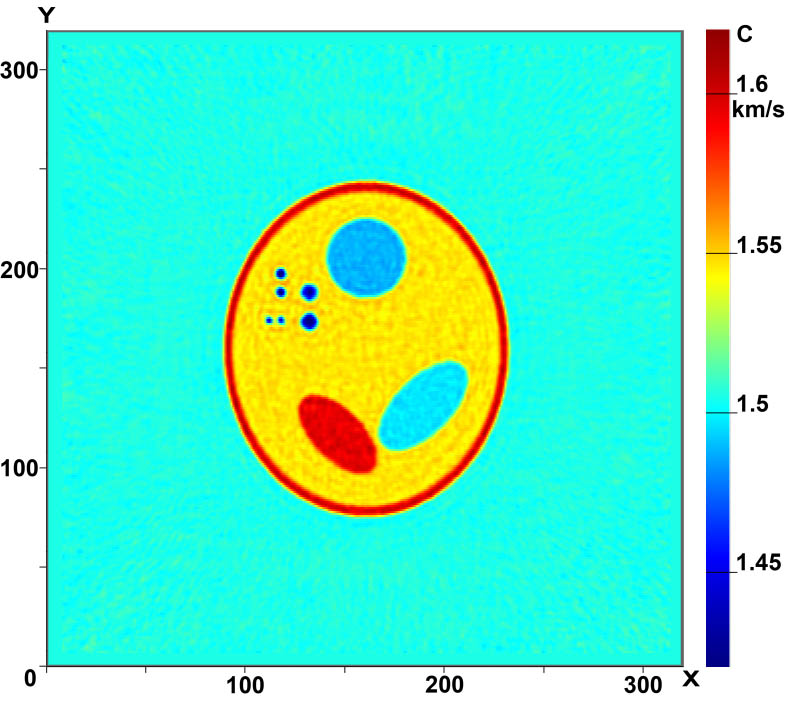
Рисунки 3 и 4 иллюстрируют возможности томографических схем в задаче 3D томографии, когда восстанавливается трехмерная функция с(x,у,z). На Рис.3 (а-в) приведены сечения трёхмерного фантома в различных плоскостях Z=const, На Рис.3 (г-е) - сечения восстановленного 3D распределения скорости звука с(x,у,z) в этих же плоскостях. В модельных расчётах использовалось 17 источников в томографической 3D схеме без элементов вращения. Расчеты проводились на сетке 320×320×320. Видно, что качество реконструкции высокое, достаточно хорошо восстанавливаются даже неоднородности размера порядка 2 мм.

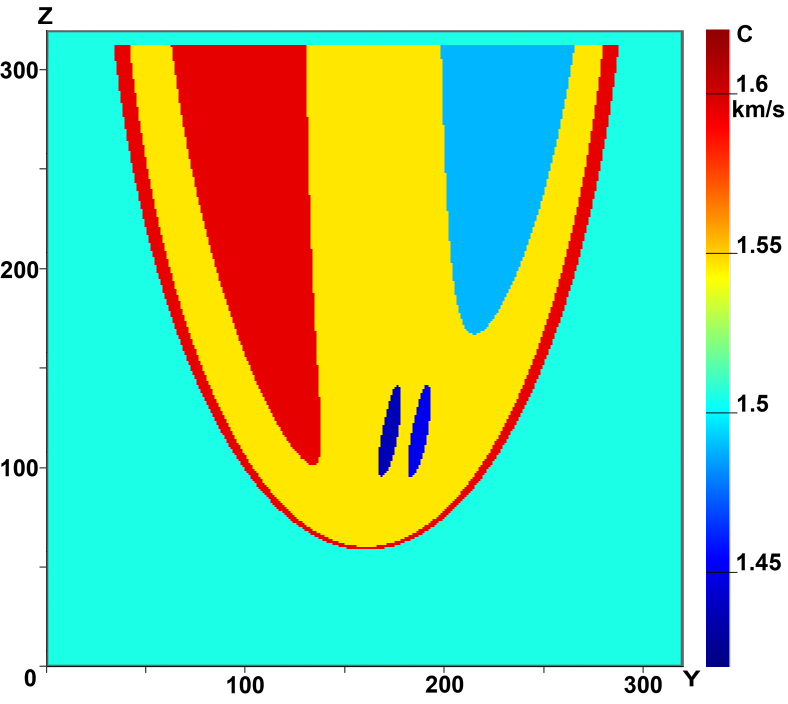
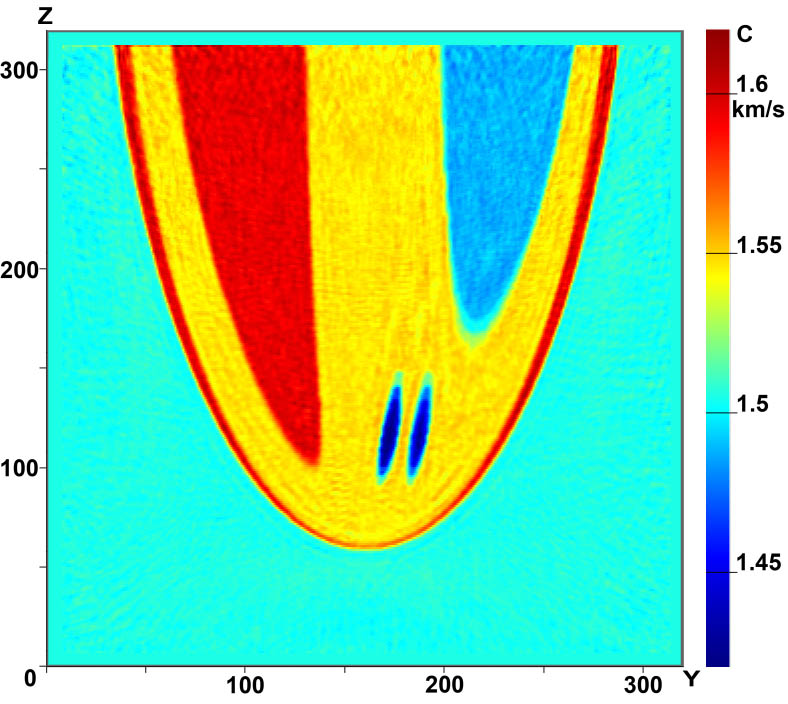
На рис.4 приведены вертикальные сечения фантома (a) и реконструированного изображения (b) в плоскости X=const.

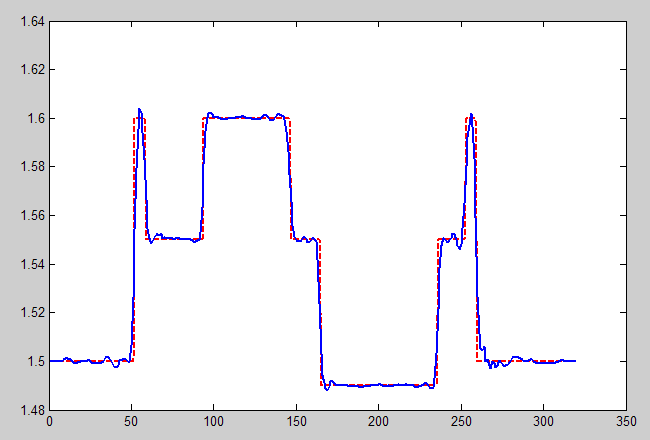
На рис.5 приведён график восстановленной скорости звука на однм из сечений A-A (рис.3д). Видно, что достигается высокая точность реконструкции абсолютных значений функции скорости звука. Восстановленное значение изображено сплошной линией, точное (фантом) - пунктирной. Все расчёты модельных задач проводились с начального приближения c₀(r)=const. Отметим, что использование традиционных ультразвуковых установок, работающих на отражение, в принципе не даёт возможности восстановления абсолютного значения скорости распространения звука в неоднородной среде.

Решение нелинейных трехмерных обратных задач УЗИ томографии невозможно без использования суперкомпьютеров. Разработанные алгоритмы решения обратных задач являются сверхмасштабируемыми на суперкомпьютерах петафлопсного уровня на процессорах общего назначения и испытаны на суперкомпьютере «Ломоносов» Суперкомпьютерного комплекса МГУ (Россия, Москва). Однако суперкомпьютеры общего назначения по своим техническим характеристикам не могут быть использованы в составе ультразвуковых томографических комплексов. Разработаны эффективные алгоритмы, решающие обратные задачи ультразвуковой томографии как в послойном 2.5D варианте, так и в 3D варианте, на суперкомпьютерах с графическими процессорами (GPU). Количество параллельно используемых графических процессоров совпадает с количеством используемых источников. GPU-cуперкомпьютеры по своим техническим характеристикам вполне могут быть использованы как автономные вычислители в составе томографических комплексов.

В лаборатории разработано открытое кросс-платформенное программное обеспечение .WaveTomography для решения прямых и обратных задач волновой томографии в послойном варианте.