Ultrasonic tomography

Inverse problems of wave tomography arise in various applications. These include some of the inverse problems of electromagnetic sounding, seismology, civil engineering, sonar, industrial diagnosis via acoustic radiation, etc.

One of the major applications of wave tomography is ultrasound tomography in medicine. The primary task of ultrasound tomography is to perform differential diagnosis of breast cancer – one of the most urgent problems in modern medicine. More than 40% of the patients have advanced breast cancer diagnosed at the first examination.

Prototypes of ultrasound tomography devices, which have a number of advantages over magnetic-resonance and x-ray tomography, are now developed extensively in the USA, Germany, Japan, and Russia [1, 2, 3], Mathematically, the inverse problems arising in ultrasound tomography are much more challenging compared to those of x-ray tomography. Ray optics model works well in x-ray tomography where inverse problems are linear and can be solved on a common PC.

Unlike x-ray tomography, ultrasound tomography uses both transmitted and reflected radiation emitted by broadband sounding sources. Detectors and sources are placed on all sides of the object examined and the signal is recorded as a time series, which makes it possible to process a very large volume of data, allowing high resolution to be achieved.

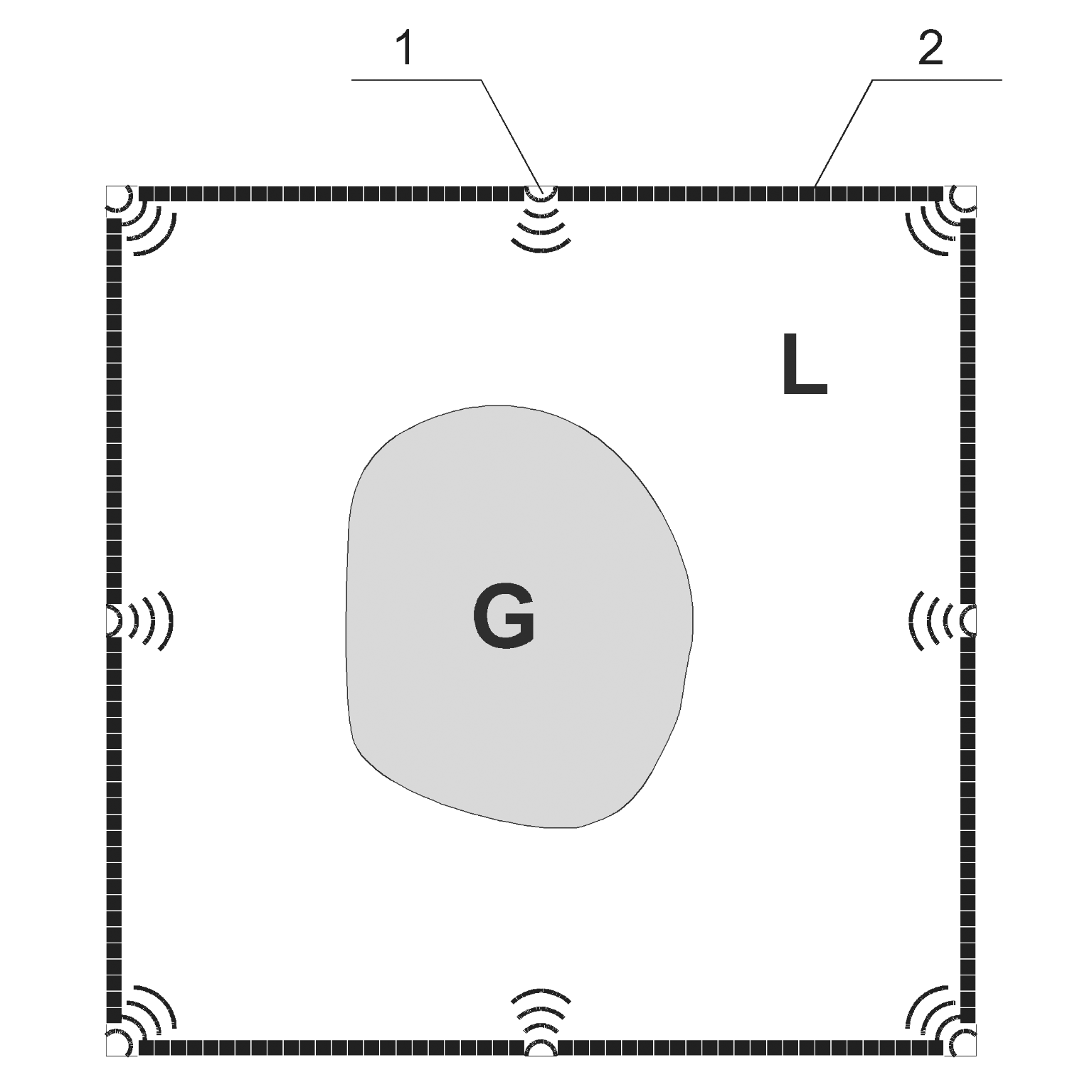
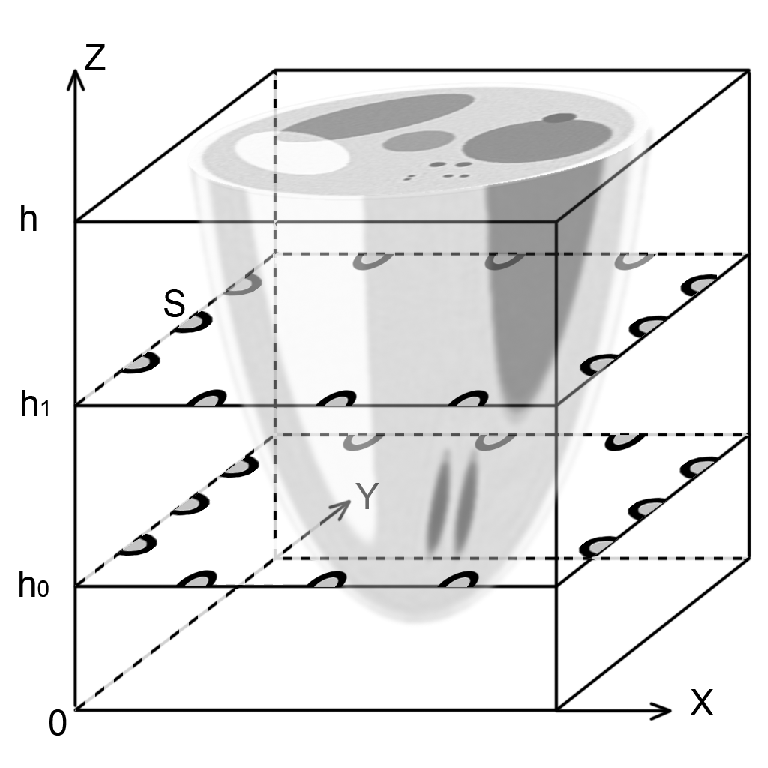
Inverse problems of ultrasound tomography can be treated as coefficient inverse problems. Let us now describe the formulation of the inverse problem. Figure 1(a) shows the schemes of tomographic experiments in the case of traditional layer-by-layer ("2.5D") tomography, where two-dimensional problems are solved on layers of a three-dimensional object. Figure 1(b) shows the scheme of 3D tomography, where the acquired experimental data are used to solve the inverse problem right away for the three-dimensional unknown function c(r), r∊R³. In Figure 1(a) the sources are labeled by digit "1" and the detectors arranged along the perimeter of the computational domain are labeled by digit "2". The sources S and detectors of ultrasound pulses in Figure 1(b) are located on the faces of the cube.

Consider now the wave equation that describes the acoustic pressure field u(r,t) in the domain Ω⊂R^N, N=2,3, confined by surface S over the time interval (0,T) with a point source located at a point r₀ .

c(r)u_tt(r,t)-Δu(r,t)=δ(r-r₀)˙f(t)

u(r,t=0)=u_t(r,t=0)=0,   ∂_nu|_ST=p(r,t).

Here c^-0.5(r)=v(r) is the unknown wave velocity in the diagnosed region. The pulse generated by the source is described by the given function f(t), ∂_nu|_ST is the derivative along the normal to surface S in region S×(0,T), and p(r,t) is a known function. We further assume that the inhomogeneity of the medium is due solely to velocity variations, and outside the inhomogeneity region c(r)≡c₀=const, where c₀ is known. The inverse problem consists in finding a function c(r) that describes the inhomogeneity given the measurements of acoustic pressure U(r,t) at the boundary S of the domain Ω with various source positions r₀ . The inverse problem is nonlinear. The number of unknowns to be determined when solving the inverse problem of ultrasound tomography on a 320×320×320 grid exceeds 10 million.

Mathematically the inverse problem is formulated as the problem of minimization of the residual functional Φ(u(c)) in the norm of L₂ space  (S×(0,T)):

		T
Φ(u(c))=	1 2	∫	∫	(u(s,t)-U(s,t))2ds dt = ||u(s,t)-U(s,t)||2
		0	S

The breakthrough results in the solution of ultrasound tomography problems are associated with the possibility of explicitly, analytically formulating the gradient of the residual functional [4, 5, 6]. The approach that we propose differs fundamentally from those currently employed [1-3], which use substantially higher sounding frequencies. The iterative algorithms that we developed to solve inverse problems of ultrasound tomography and the simulations performed over a wide range of parameter values allow the sounding frequencies to be reduced several times. This point is of fundamental importance, because attenuation in soft tissues depends heavily on sounding frequency. The lower the frequency, the smaller the attenuation, and hence the smaller the error of experimental data. Simulations show that about 5-mm wavelength ultrasound allows a resolution of about 2-3 mm to be achieved. In our paper [7] we propose efficient methods to solve inverse problems of ultrasound tomography in terms of models that take into account attenuation in the medium.

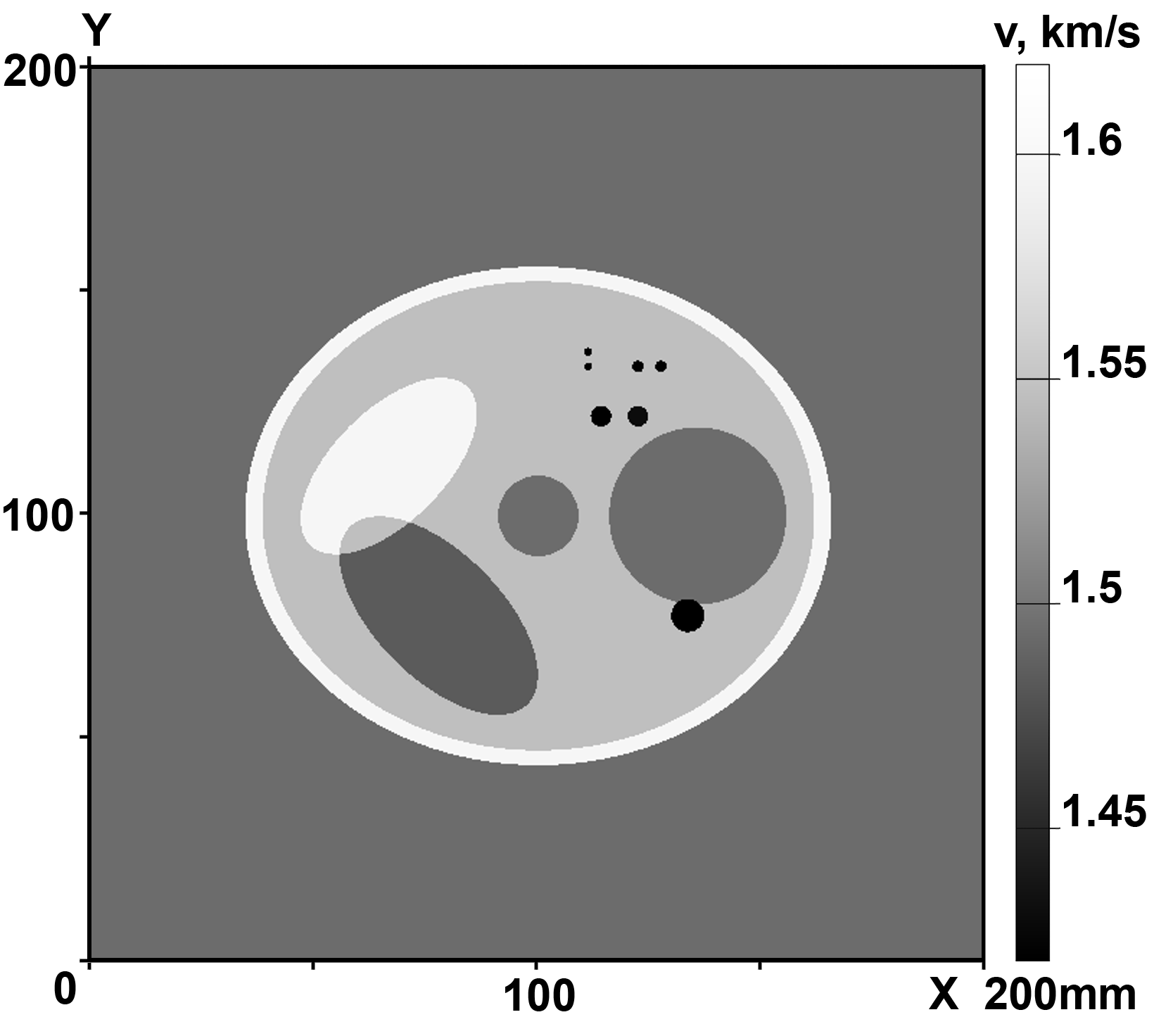
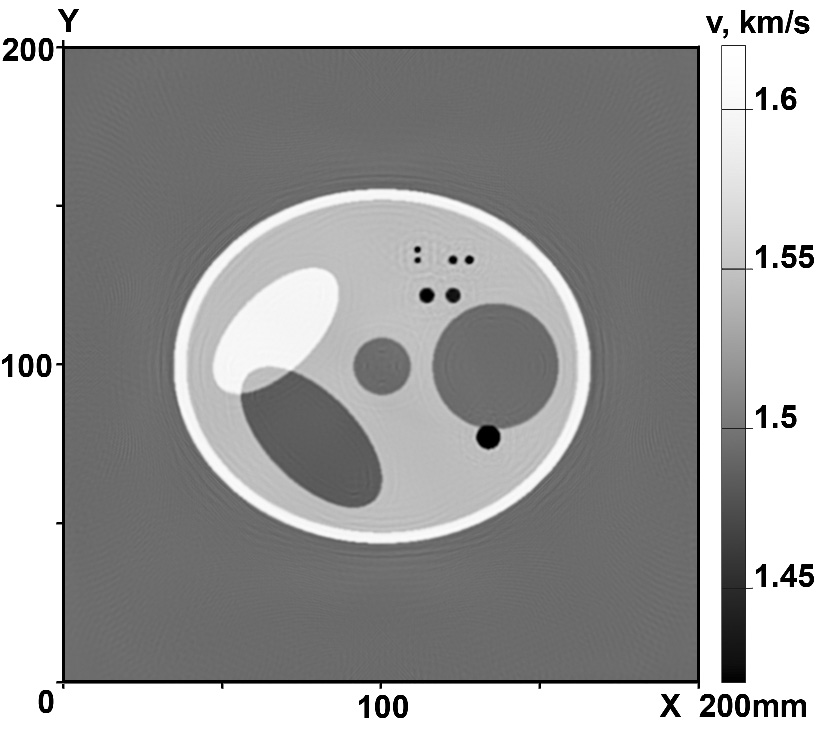
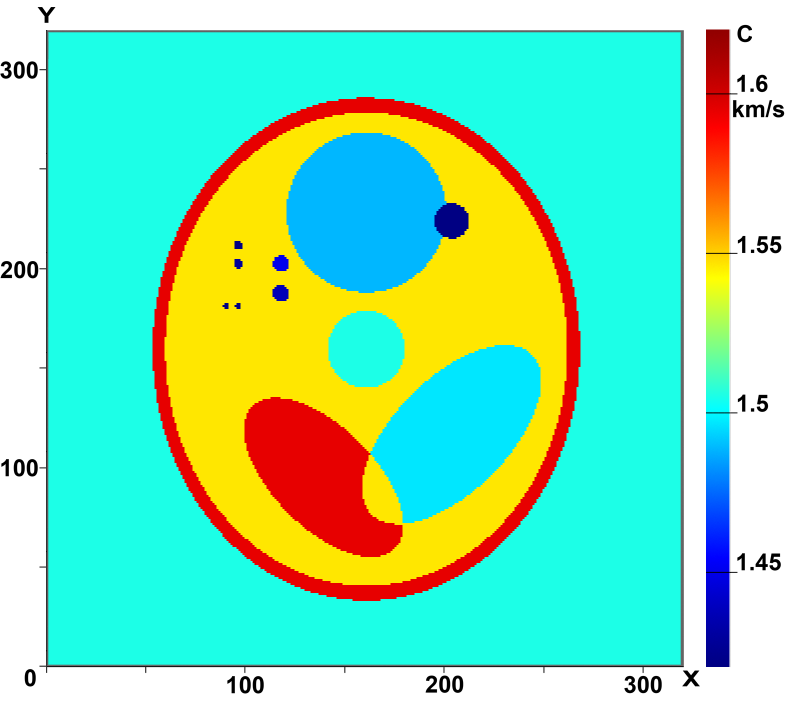
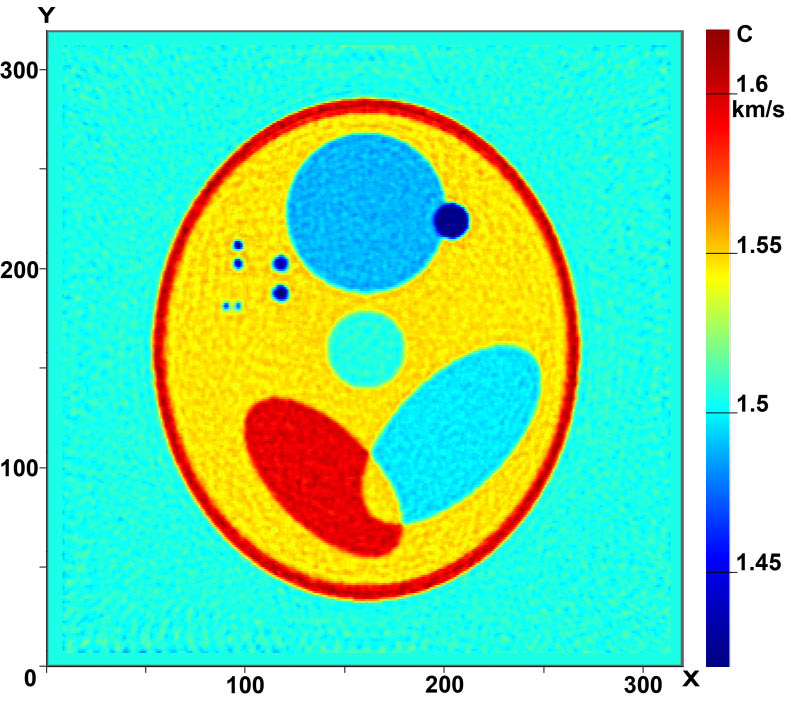
Figure 2 shows the results of the reconstruction in the case of layer-by-layer tomography. Figure 2(a) shows the image of a 2D phantom. Figures 2(b) and 2(c) show the reconstructed velocity structure in the case of zero- and 1.5%-error input data, respectively. The simulations were performed for eight sources with the detectors spaced 2.5 mm, i.e., half the wavelength, apart. The size of the sounding region is 200×200 mm.

The minimum size of inhomogeneities in the phantom is about 2 mm. As is evident from a comparison of the initial and reconstructed images, the resulting resolution is 2-3 mm or better.

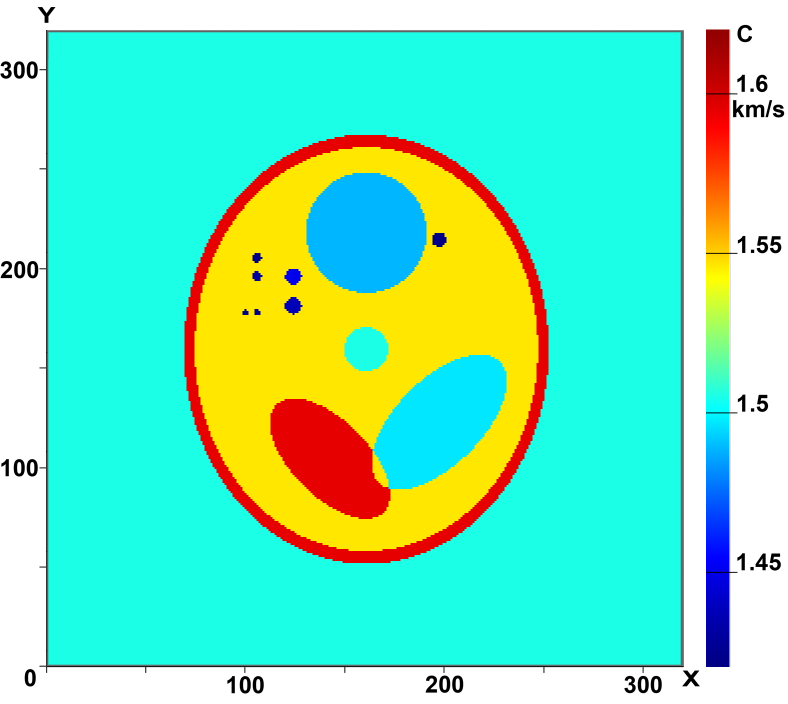
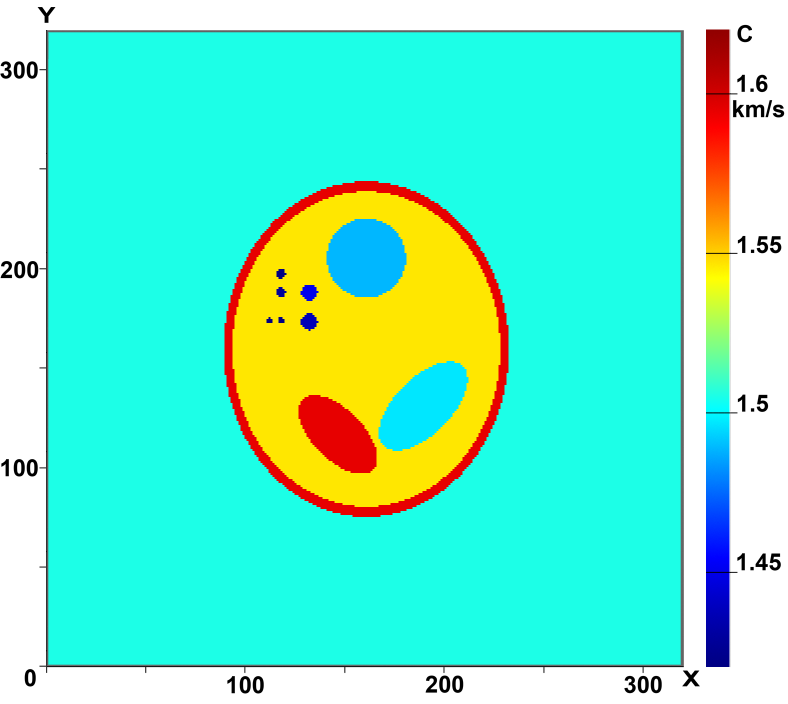
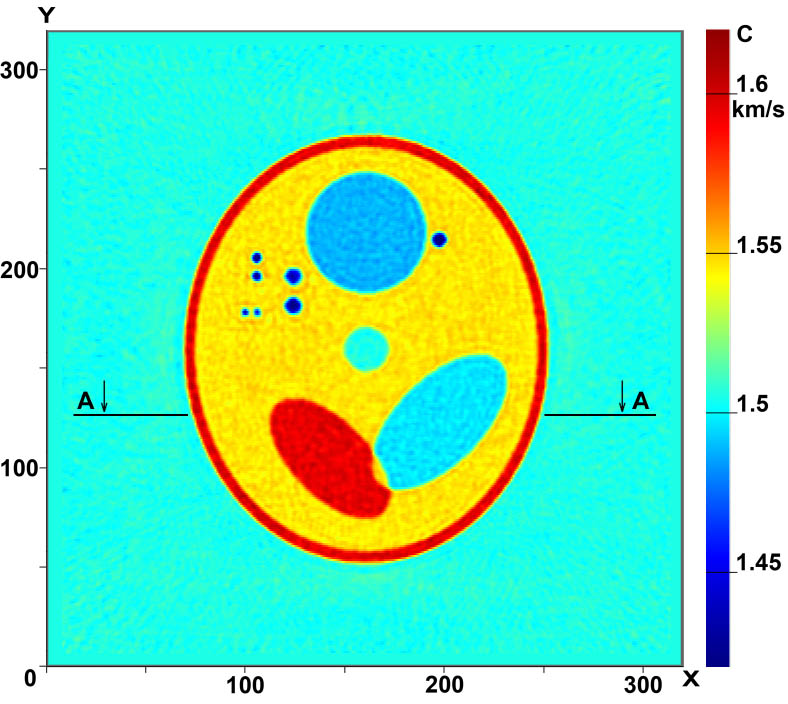
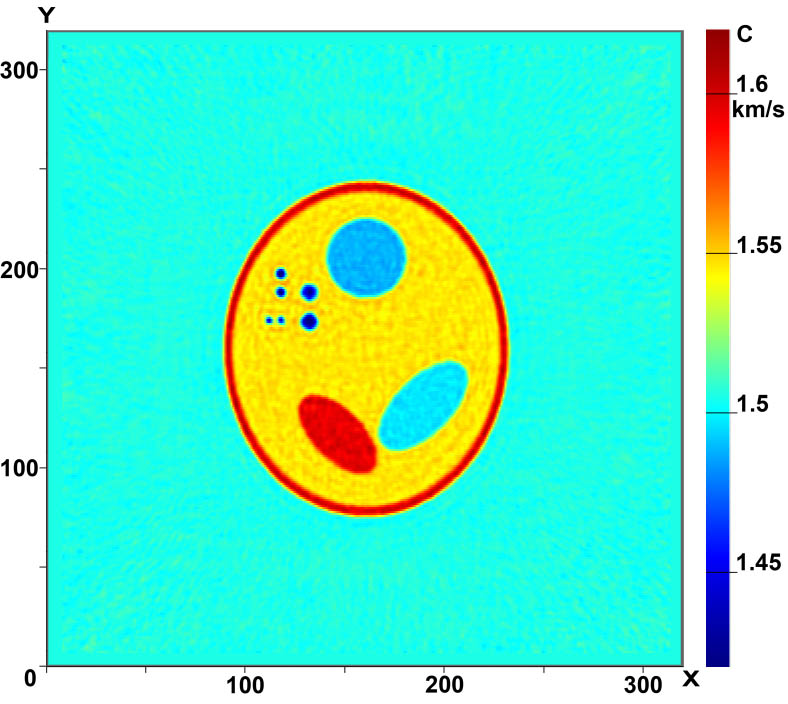
Figures 3 and 4 illustrate the capabilities of 3D tomographic schemes involving the reconstruction of the three-dimensional function с(x,у,z). Figures 3 (a-c) shows the cross sections of the three-dimensional phantom in several planes Z=const and Fig.3 (d-f), the cross sections of the reconstructed 3D velocity structure с(x,у,z) in the same planes. In our simulations we used 17 sources in a 3D tomography scheme without elements of rotation. The computations were performed on a 320×320×320 grid. As is evident from the figures, the quality of reconstruction is high, allowing inhomogeneities as small as 2mm to be reconstructed fairly well.

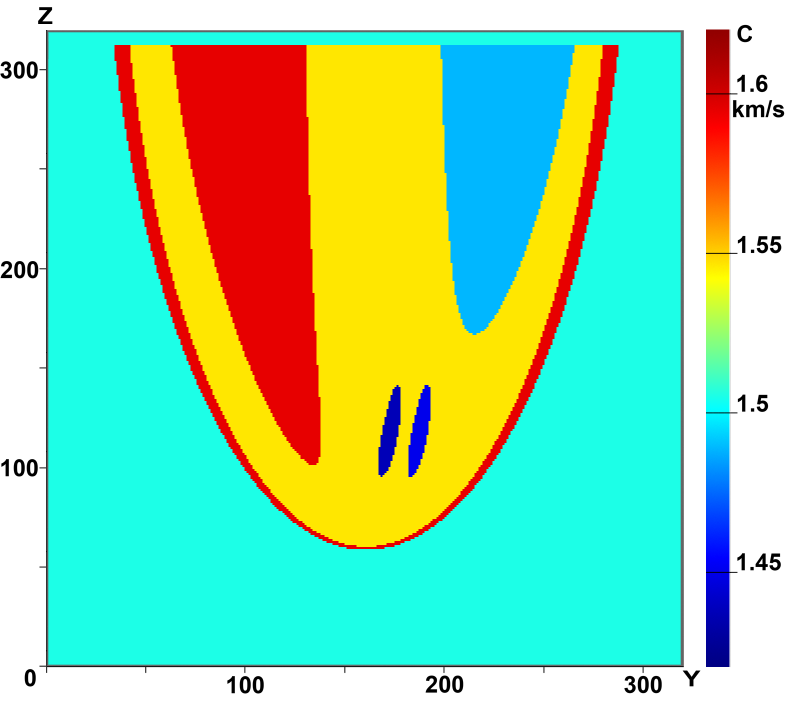
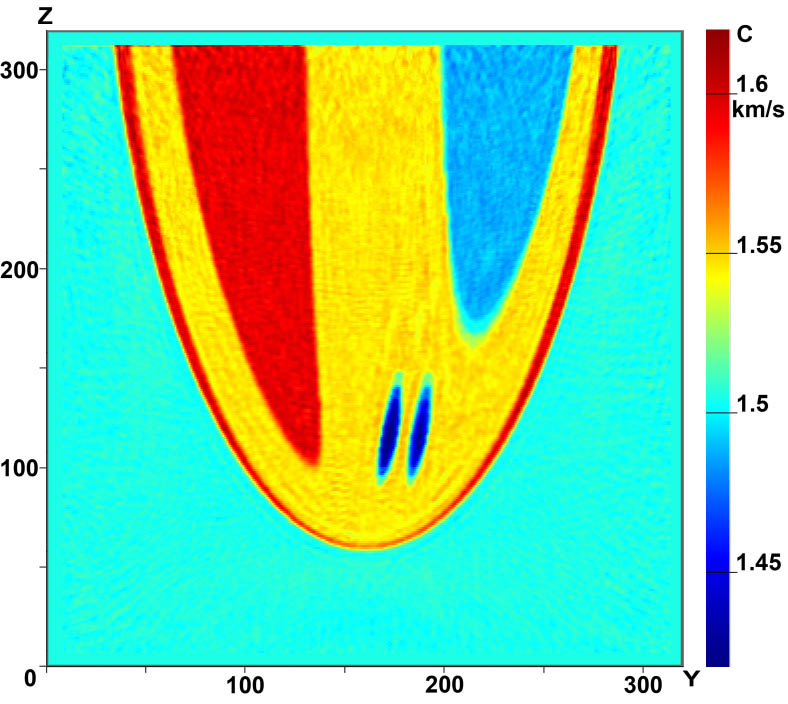
Figure 4 shows the vertical cross sections of the phantom (a) and of the reconstructed image (b) in the X=const plane.

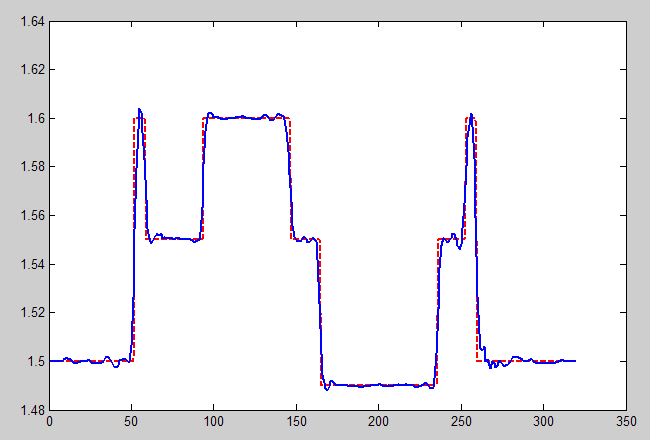
Figure 5 shows the profile of the reconstructed sound velocity structure along one of the A-A cross sections (shown in Figure 3(e)). As is evident from the figure, the absolute sound velocity values are reconstructed very accurately. The reconstructed and exact (phantom) sound velocity values are shown by the solid and dashed lines, respectively. We started all our simulations with the initial approximation c₀(r)=const. Note that common ultrasound facilities operating in the reflection mode are in principle incapable of reconstructing the absolute value of sound velocity in an inhomogeneous medium.

Three-dimensional inverse problems of ultrasound tomography can be solved only with supercomputers. The algorithms that we developed to this end are highly scalable, up to petaflops-level supercomputers based on general-purpose processors, and were tested on "Lomonosov" supercomputer of Moscow State University Supercomputing Center (Moscow, Russia). However, because of their technical parameters, general-purpose supercomputers cannot be incorporated into ultrasound tomographic facilities. We developed efficient algorithms that allow inverse problems of ultrasound tomography both in the layer-by-layer 2.5D and explicit 3D formulation to be solved on GPU-based supercomputers. The number of parallel operating graphical processors is equal to that of the sources employed. The technical parameters of GPU-based supercomputers allow them to be incorporated into tomographic facilities as autonomous computing units.

Open-source cross-platform "WaveTomography" software has been develped in this laboratory for solving direct and inverse problems of wave tomography in the 2D formulation.